SZEREGOWANIE ZADAŃ NA POJEDYNCZEJ MASZYNIE

W przypadku problemu jednomaszynowego rozwiązanie optymalne otrzymuje się stosując jedną z czterech najczęściej stosowanych kryteriów optymalizacji, a mianowicie:

• dowolną regułę w przypadku minimalizacji długości uszeregowania.
• regułę SPT w przypadku minimalizacji średniego czasu przepływu.
• regułę EDD w przypadku minimalizacji maksymalnego opóźnienia.
• dla problemu minimalizacji średniego spóźnienia nie istnieją tak proste algorytmy. Niżej pokazano jak można rozwiązać ten problem, a właściwie równoważny problem minimalizacji sumy spóźnień, za pomocą metody podziału i oszacowań.

Metoda podziału i oszacowań

Jeśli mamy jakiś problem optymalizacji dyskretnej, której cechą jest skończoność zbioru rozwiązań dopuszczalnych, to jedną z możliwości znalezienia rozwiązania optymalnego jest metoda przeglądu zupełnego. Jednak takie postępowanie dla dużej liczby rozwiązań jest bardzo czasochłonne i niepraktyczne. Pożądane są więc procedury przeglądu niezupełnego, umożliwiające wyłączenie z poszukiwań jak największych podzbiorów zbioru rozwiązań dopuszczalnych, przy zachowaniu pewności, że nie eliminuje się w ten sposób rozwiązania optymalnego. W najgorszym jednak przypadku do uzyskania rozwiązań jednostkowych będziemy potrzebować przeglądu zupełnego. Pewnym schematem tego typu procedur jest metoda podziału i oszacowań (algorytm)

Za pomocą metody podziału i oszacowań możemy minimalizować sumę spóźnień poszczególnych zadań na pojedynczej maszynie. Zmienną decyzyjną, której wartości są elementami zbioru rozwiązań dopuszczalnych, jest permutacja S zadań wykonywanych na pojedynczej maszynie kolejno i bez przerw czasowych. Przy znanych oznaczeniach, dla problemów jednomaszynowych funkcja celu dana jest wzorem:

Jeśli w uszeregowaniu S zadanie j jest k - te w kolejności, czyli [k] = j, a  t_j jest czasem wykonania zadania j, to:

Skreślenie z listy podzbioru rozwiązań jako nieoptymalnego odbywa się na zasadzie sprawdzenia dolnego oszacowania wartości podproblemu:

gdzie R jest znaną, konkretną sekwencją zadań ustawionych na ostatnich k pozycjach.

Aby zrozumieć problem przyjmiemy następujące oznaczenia:

P            - problem optymalizacji dyskretnej,
F(P)       - skończony zbiór rozwiązań dopuszczalnych problemu P,
v(P)       - wartość problemu P, czyli optymalna wartość funkcji celu y,
y            - funkcja celu, kryterium optymalizacji,
x            - zmienna decyzyjna.

Rozwiązanie optymalne problemu P może być znalezione przez przegląd rozwiązań optymalnych podproblemów, z których każdy dotyczy jednego z rozłącznych podzbiorów zbioru rozwiązań dopuszczalnych problemu P, przy zachowaniu funkcji celu z problemu P.

Stąd:

1. Jeśli rozwiązanie optymalne podproblemu Pi jest znane, to:
   • należy go zapamiętać wraz z wartością funkcji celu, jeżeli jest lepsze od dotychczas najlepszego ze sprawdzonych rozwiązań dopuszczalnych,
   • należy go odrzucić, wraz z całym podproblemem Pi , gdy nie jest lepsze od dotychczas najlepszego rozwiązania problemu P.
2. Jeśli rozwiązanie podproblemu Pi nie jest znane, to:
   • można skreślić podproblem Pi, gdy znane jest dolne oszacowanie bi wartości v(Pi) i jest ono większe lub równe od dotychczas najlepszej (czyli najmniejszej) wartości y* funkcji celu y,
   • należy podzielić zbiór rozwiązań dopuszczalnych podproblemu Pi na podzbiory rozłączne i dopisać tak powstałe nowe podproblemy do listy oczekujących na analizę, równocześnie skreślając z niej podproblem Pi  

Metoda podziału i oszacowań znana jest bardziej pod nazwą "metoda podziału i ograniczeń". Słowo "podział" dotyczy podziału zbioru rozwiązań dopuszczalnych. Słowo "ograniczeń" reprezentuje dolne oszacowania optymalnych wartości funkcji celu w podproblemach.

Mamy dwie strategie przeszukiwania drzewa podproblemów:

Backtracking - metoda zagłębiania - wybór z listy podproblemów ograniczony do podproblemów o największej liczbie ustalonych elementów, sprzyja szybkiemu znajdowaniu rozwiązań próbnych. Jest to strategia czasochłonna, gdyż przeszukujemy większą ilość podproblemów. Można to zauważyć w przykładzie przedstawionym na końcu.
Jumptracking - metoda poszerzania - wybór spośród wszystkich podproblemów znajdujących się na liście. Ten sposób wymaga pamiętania dłuższej listy, ale na ogół osiąga rozwiązanie optymalne po mniejszej liczbie podziałów.
Zbiór dominujący uszeregowań dopuszczalnych jest to taki podzbiór zbioru wszystkich uszeregowań dopuszczalnych, o którym wiadomo, że zawiera rozwiązanie optymalne. W rozpatrywanym problemie, jeśli termin zakończenia jednego z zadań jeszcze nieustawionych jest większy niż suma czasów wykonania wszystkich tych zadań, czyli gdy:

Zazwyczaj gdy rozwiązujemy jakiś problem metodą podziału i oszacowań, to wykres czasowy który otrzymamy, porównujemy z wykresem czasowym metody EDD. W ten sposób widzimy, która z metod jest lepsza. Należy tu zaznaczyć, że wykres otrzymany  metodą EDD jest dużo prostszy w realizacji, a przede wszystkim szybciej go można wykonać.

Reguła EDD

Dla reguły EDD ( ang. earliest due time ) maksymalne opóźnienie L_max i maksymalne spóźnienie T_max są minimalne. Priorytetem w tej sytuacji jest najwcześniejszy termin wykonania. Algorytm ten każdorazowo przydziela operację o najwcześniejszym terminie ukończenia do aktualnie wolnej maszyny. Reguła ta znana jest również jako reguła Jacksona.

gdzie:
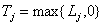
	- opóźnienie zlecenia j
	- spóźnienie zlecenia j
	- pożądana chwila zakończenia (termin zamknięcia) zlecenia
	- chwila zakończenia zlecenia j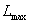
	- maksymalne opóźnienie

 

Stosując regułę EDD, zauważymy na poniżej przedstawionym przykładzie, że wynik różni się od metody podziału i oszacowań, i w dwóch przypadkach zadania nie są w stanie skończyć się w pożądanym przez nas terminie. 

Aby narysować wykres musimy znać sekwencję zadań, które są wykonywane jedno po drugim. Do tego celu bierzemy pod uwagę pożądane chwile zakończenia zlecenia dj i ustawiamy je w kolejności rosnącej. Mając tak ustawione zadania, odczytujemy sekwencję zgodnie z j.

Przykład